また，式 から波動方程式 を得ますが，この解は，速度 で移動する波を与えます．この は光速（つまり光は電磁波です）なのですが，この記事では，電磁気学の内容には深入りせず，専らマックスウェルの方程式を微分形式で表わすことだけ考えます．そういうわけで，電磁気学を全然知ら3章 1次方程式 2．1次方程式の応用 1方程式を利用した文章題の解法の手順 ①問題をよく読み、わからない数量を\(x\) とおく。 ②等しい数量の関係をみつけて、方程式を作る。 ③方程式を解く。 ④方程式の解が問題に適しているか確かめる。方程式の応用 目次 > 距離（道のり）を求めてみましょう。方程式の応用 目次 > 距離（道のり）を求めてみましょう。 距離は、直線の長さや曲線の長さを表します。道のりは、道に沿った長さです。 距離（道のり）＝速さ×時間 です。(
方程式 の 応用" /> 中学2年数学 連立方程式 連立方程式の応用 練習問題2 あんのん塾
方程式 の 応用
方程式 の 応用-また，式 から波動方程式 を得ますが，この解は，速度 で移動する波を与えます．この は光速（つまり光は電磁波です）なのですが，この記事では，電磁気学の内容には深入りせず，専らマックスウェルの方程式を微分形式で表わすことだけ考えます．そういうわけで，電磁気学を全然知ら6 物理現象と微分方程式 重力下の質点の運動（時間的変化） z運動方程式 （ニュートン第2法則） z落下量（位置，変位）x(t) の時間t による微分 Ö1階微分 ：速度 Ö2階微分 ：加速度 Ö微分方程式 ： ＋初期条件： Ö解（質点の落下量）： ma F mg⋅ == 2 2 dx mmg
方程式 の 応用"> 
高校数学 ２次 ３次方程式の応用問題 ２ 練習編 映像授業のtry It トライイット
3章 1次方程式 2．1次方程式の応用 1方程式を利用した文章題の解法の手順 ①問題をよく読み、わからない数量を\(x\) とおく。 ②等しい数量の関係をみつけて、方程式を作る。 ③方程式を解く。 ④方程式の解が問題に適しているか確かめる。微分方程式(425)の一般解となっている。 この計算では、方程式(425)がy について線形であるために、y1, y2 それぞれだけについての式に 分解できることを使っている。また、式の最後の行では式(427)、すなわちy1;y2 のそれぞれが式 (425)の解であることを用い路の解析には古くから常微分方程式の定性論や力学 系†の理論が用いられてきた．例えば，発振回路の 安定な自励振動のモデルとしてのvan der Pol 方程 式（†1）や非線形インダクタを含む回路に正弦波電 源を印加した回路のモデルであるDuffing 方程式†
動画一覧や問題のプリントアウトはこちらをご利用ください。ホームページ → http//19chtv/ Twitter→ https//twittercom/haichi_toaru数学33章二次方程式「二次方程式の利用」＜応用問題①＞ 組 番 名前 千葉君は，メッセージを書くために，縦8㎝，横10㎝の紙を用意しましたが，やや大きかっ たため図のように周囲を同じ幅で切り取りました。すると面積が48㎝2となりました。切り取っマックスウェル方程式への応用 2 r£ B = j @E @ct (24) 三次元ユークリッド空間上の微分形式 最初に，微分形式の復習も兼ねて，三次元ユークリッド空間上で次のような一次微分形式E;J と二次 微分形式B を考えてみます． E = Exdy ^ dz Eydz ^ dx Ezdx ^ dy (31) B = Bxdx Bydy Bzdz (32) j = Jxdy ^ dz Jydz ^ dx
応用問題 基本解答 応用解答 式と証明 数列 整式の除法 等差数列 分数式 等差数列の和 恒等式 等比数列 等式の証明 等比数列の和 不等式の証明 和の記号Σ 方程式と不等式 階差数列 複素数とその演算 いろいろな数列の和 2次方程式と解と係数シュレーディンガー方程式（シュレーディンガーほうていしき、英 Schrödinger equation ）とは、物理学の量子力学における基礎方程式である。 シュレーディンガー方程式という名前は、提案者であるオーストリアの物理学者 エルヴィン・シュレーディンガーにちなむ。微分方程式は方程式に含まれる導関数の階数 によって分類され、最も高い階数が n 次である場合、その微分方程式を n 階微分方程式 と呼ぶ 。 いずれの場合も未知関数は一つとは限らず、また、連立する複数の微分方程式を同時に満たす関数を解とするよう
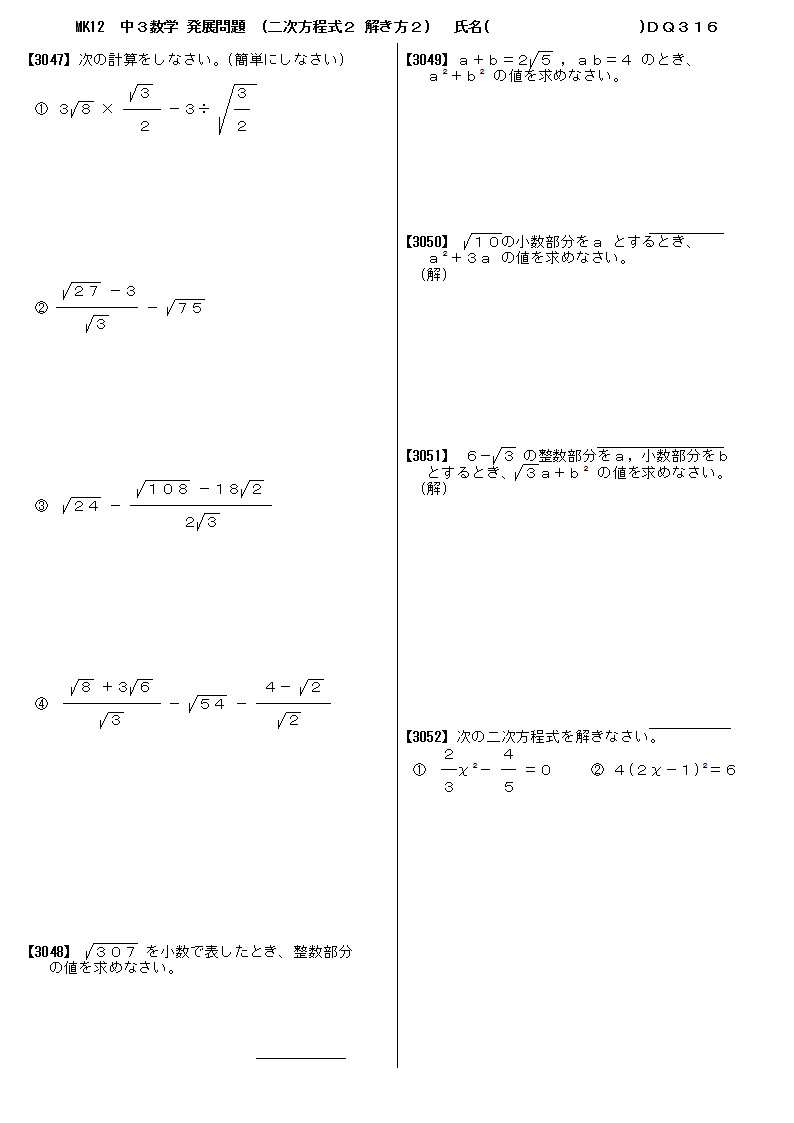
方程式 の 応用"> 無料 中３数学 発展 応用問題 問題プリント 316 ２次方程式２ 解き方２
方程式 の 応用"> 方程式の応用 高校数学に関する質問 勉強質問サイト
「連立方程式の利用」の文章題を一目で理解できるように、重要事項を最も簡単にまとめました。 1、問題を解くときの順序 (1)何をxとyにするかを決める（ふつう、問題文の最後で「求めなさい」と書かれているものをx、yにする） (2)問題文中で、「文章を等式に表せる部分」を2か所見つけて確率微分方程式の数値解析とその応用 田口 大 確率微分方程式の理論は，伊藤清氏によって確立され，数学の中に留まらず， 数理ファイナンス，物理学，生物学など様々な分野で重要な役割を担う理論となっています．また，近年，数理ファイナンスの研究は，理論・実務の両側面から盛んに42 二階定数係数斉次常微分方程式 本節以降では、未知関数y(x)の二階微分を含む微分方程式を取り扱う。最も簡単な例を挙げると y′′ = 0 (421) これは、次のようにx積分を2回行うことで解y(x)が得られる。 d2y dx2 = 0 (422)
方程式 の 応用"> 二次方程式の応用 高校数学に関する質問 勉強質問サイト
方程式 の 応用"> 中学2年数学 連立方程式 連立方程式の応用 練習問題2 あんのん塾
② 応用方程式 応用方程式 とは、 次の状態 Q n を 現在の状態 Q と 入力 を用いて表現したものであり、一般に次のように表されます。 この式で、 g 1 、 g 2 という変数は 0 または 1 の値をもつ 論理関数 です。 g 1 、g 2 は設計する順序回路に依存し、 その入力 の関数になります。方程式の応用 目次 > 距離（道のり）を求めてみましょう。方程式の応用 目次 > 距離（道のり）を求めてみましょう。 距離は、直線の長さや曲線の長さを表します。道のりは、道に沿った長さです。 距離（道のり）＝速さ×時間 です。(判別式を用いた応用問題 判別式"D＝b²−4ac"を使った応用問題を一緒に解いてみましょう。 問題 2次方程式"2x²＋2mx＋2m＋4＝0"が重解をもつような定数mの値を求めましょう。そしてそのときの重解
方程式 の 応用"> 楽天ブックス 微分方程式とその応用新訂版 竹之内脩 本
方程式 の 応用"> 偏微分方程式までの応用数学 Mathematica で検証する 訂正
もう2次方程式の応用問題の悩みから解放されます。 下記のことが理解できると、 あなたは、たちまち本物の実力がつき始めます。 あなたの実力を1分以内に確実に上げます。 本物の勉強は、ここがスタートラインです。｢ のとき \ ｣ のような条件が与えられると，微分方程式の解に含まれる定数の値を定め ることができる。このような条件を，微分方程式の 初期条件 という。 積分とその応用微分方程式 1GFD ワークノート 振動方程式への応用 2 この時, Un = U0j jnein (5) とかける 安定性は以下の様に評価される j j > 1 不安定 j j = 1 中立 j j < 1 減衰 位相については, 真の解の位相と数値解の位相との比をとって評価する
方程式 の 応用"> 明倫館書店 応用数学叢書 15冊セット揃い
連立方程式の応用 1 3全てわからないのですが解説とともに詳しく教えていただ Yahoo 知恵袋
シュレーディンガー方程式（シュレーディンガーほうていしき、英 Schrödinger equation ）とは、物理学の量子力学における基礎方程式である。 シュレーディンガー方程式という名前は、提案者であるオーストリアの物理学者 エルヴィン・シュレーディンガーにちなむ。マックスウェル方程式への応用 2 r£ B = j @E @ct (24) 三次元ユークリッド空間上の微分形式 最初に，微分形式の復習も兼ねて，三次元ユークリッド空間上で次のような一次微分形式E;J と二次 微分形式B を考えてみます． E = Exdy ^ dz Eydz ^ dx Ezdx ^ dy (31) B = Bxdx Bydy Bzdz (32) j = Jxdy ^ dz Jydz ^ dx確率微分方程式の基礎(応用数理サマーセミナー06「確率微分方程式」講演) 公開日 17 巻 1 号 p 2128
くもんの 方程式の応用問題です 小学6年にもわかるように具体的に Yahoo 知恵袋
方程式 の 応用"> 数学 中2 24 連立方程式の利用 割合の応用編 Youtube
方程式の応用 目次 > 距離（道のり）を求めてみましょう。方程式の応用 目次 > 距離（道のり）を求めてみましょう。 距離は、直線の長さや曲線の長さを表します。道のりは、道に沿った長さです。 距離（道のり）＝速さ×時間 です。(動画一覧や問題のプリントアウトはこちらをご利用ください。ホームページ → http//19chtv/ Twitter→ https//twittercom/haichi_toaru方程式の応用 目次 > 距離（道のり）を求めてみましょう。方程式の応用 目次 > 距離（道のり）を求めてみましょう。 距離は、直線の長さや曲線の長さを表します。道のりは、道に沿った長さです。 距離（道のり）＝速さ×時間 です。(
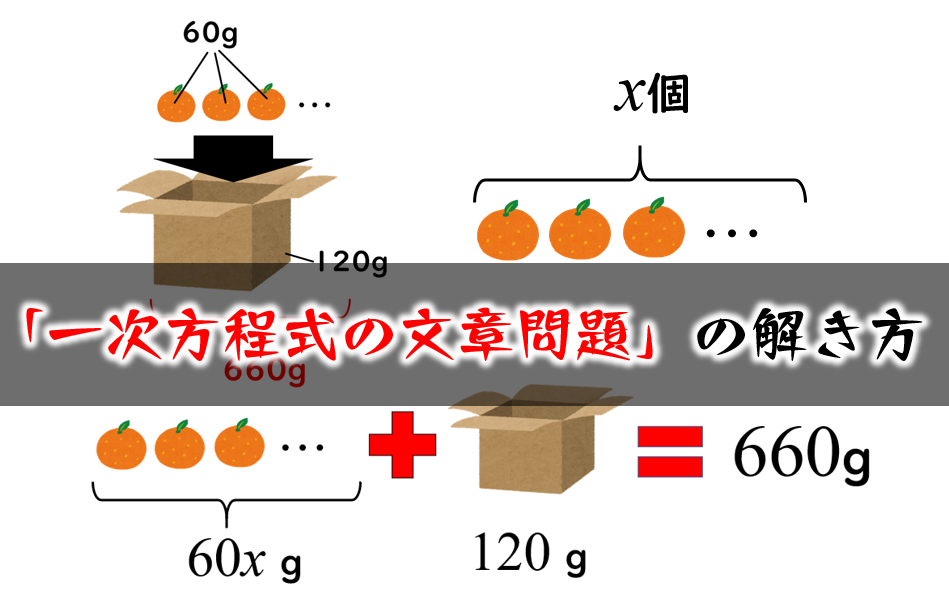
方程式 の 応用"> 一次方程式の文章問題の解き方 数学fun
方程式 の 応用"> 中学２年生 数学 連立方程式の活用 文章題 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生
指数関数を含んだ方程式の計算 前回のテキストでは、 を満たすxの値を考えながら、指数関数を含んだ方程式の解き方の基本を説明しました。今回は、試験でよく出題される応用の形をみていきましょう。 ＜問題1＞ この式を満たすxの値を求めなさい。差分方程式系への応用 名大理 巌佐正智(Iwasa Masatomo) 野崎一洋(Nozaki Kazuhiro) 概要 力学系における特異摂動法としては，これまでにさまざまなものが考案されているが，我々 は常微分方程式の有する対称性(Lie Symmetry) を利用して，その漸近解を求めるくりこみ群
方程式 の 応用"> 方程式の応用４ 速さに関する問題 算数 数学が好きになりmath
連立方程式の応用問題 中学数学教材研究ノート
方程式 の 応用"> 中学数学2年 連立方程式の応用 個数と代金 受験の月
方程式 の 応用"> 連立方程式の応用問題 中学数学に関する質問 勉強質問サイト
方程式 の 応用"> 16年度秋学期 応用数学 解析 第８回 ２階線形微分方程式 ２ 16 11 24
方程式 の 応用"> メルカリ 中２数学 連立方程式の応用問題 参考書 1 100 中古や未使用のフリマ
方程式 の 応用"> 連立方程式の応用問題 中学数学 理科 寺子屋塾の復習サイト
方程式 の 応用"> 中学数学 １次方程式 文章題の解き方 代金 個数
方程式 の 応用"> 食塩水の濃度に関する連立２元１次方程式の応用問題 中学校２年生の数学より 身勝手な主張
方程式 の 応用"> 朝倉書店 応用微分方程式
方程式 の 応用"> 応用数学 微分方程式の応用例 力学編 微分方程式 りけいのり
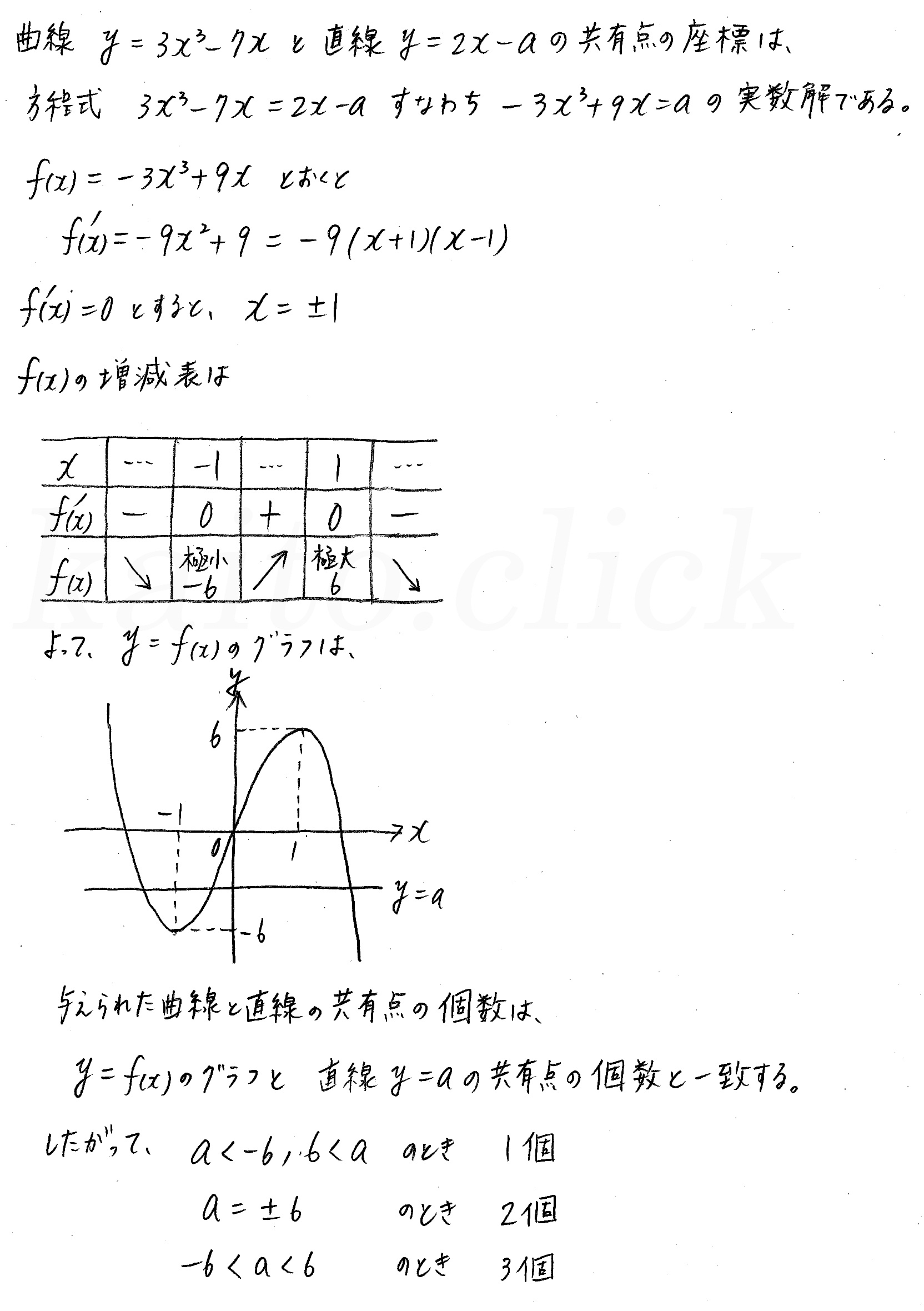
方程式 の 応用"> 高校数学 ２次 ３次方程式の応用問題 ２ 練習編 映像授業のtry It トライイット
方程式 の 応用"> 中2数学連立方程式の応用 文章題 内申 通知表を上げる西谷梅の木ユニティ
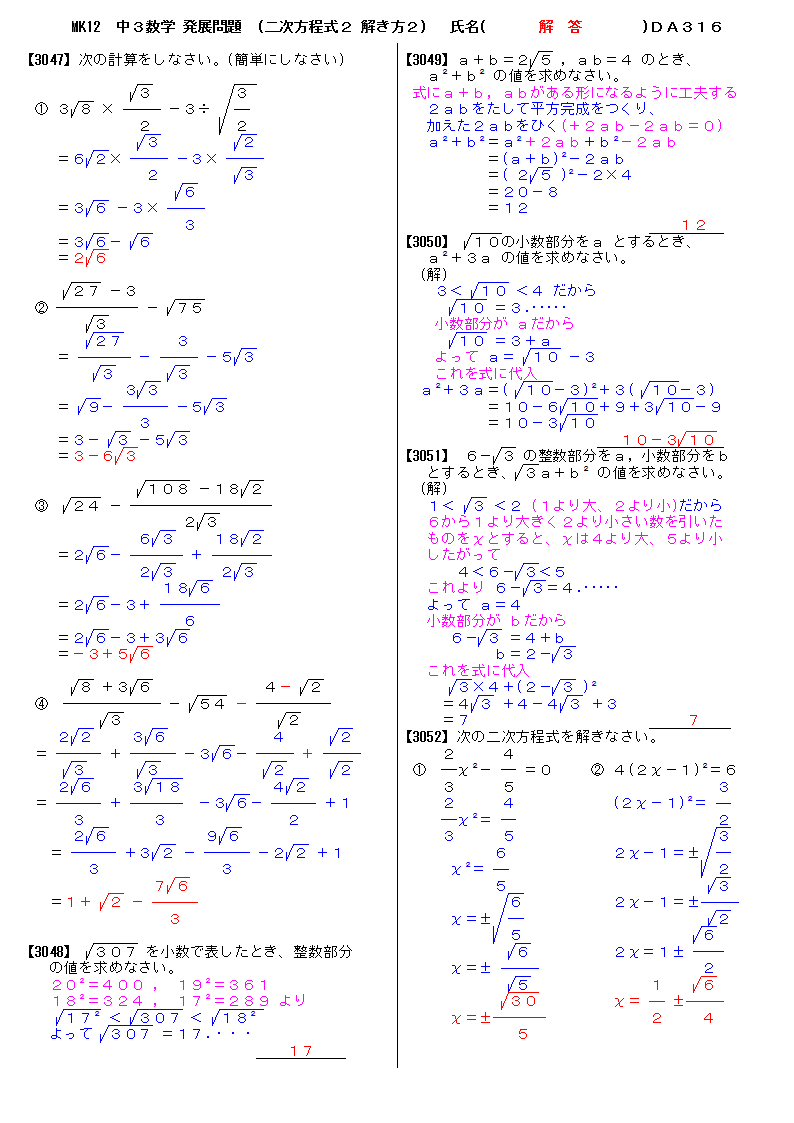方程式 の 応用"> 無料 中３数学 発展 応用問題 解答プリント 316 ２次方程式２ 解き方２
方程式 の 応用"> 連立方程式とは 代入法と加減法 計算問題や文章題の解き方 受験辞典
方程式 の 応用"> 誰でもわかる数学 中学１年 一次方程式の応用問題 Youtube
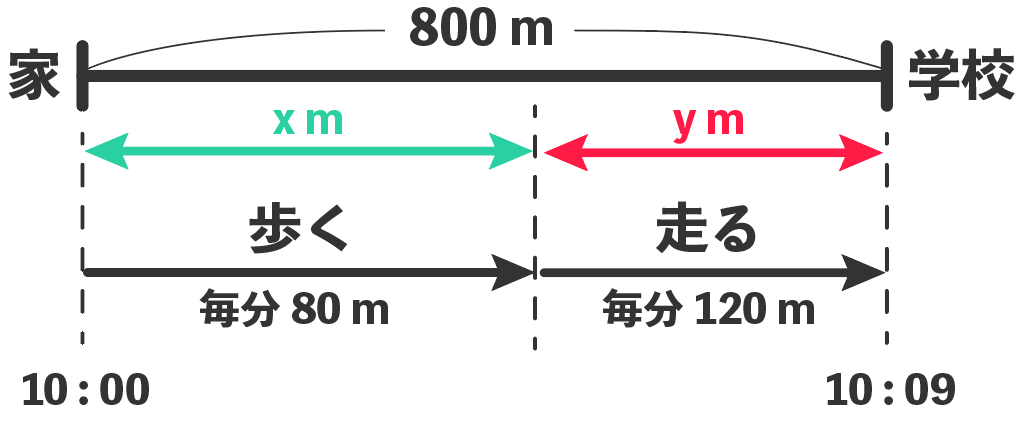
方程式 の 応用"> 連立方程式の利用 速さ 道のり 時間の文章問題の解き方 Qikeru 学びを楽しくわかりやすく
方程式 の 応用"> 方程式の応用３ 過不足に関する問題 算数 数学が好きになりmath
方程式 の 応用"> 一番欲しい 中学 数学 連立 方程式 ここから印刷してダウンロード
方程式 の 応用"> 誰でもわかる数学 中学１年 一次方程式の応用問題 Youtube
方程式 の 応用"> 連立方程式の応用問題の文章問題は どうやったら簡単にとけるようになりますか Clear
方程式 の 応用"> Studydoctor速さ 連立方程式の文章題 中２数学 Studydoctor
方程式 の 応用"> 中2数学連立方程式の応用 文章題 内申 通知表を上げる西谷梅の木ユニティ
方程式 の 応用"> ２次方程式の文章題ー図形の問題 無料で使える中学学習プリント
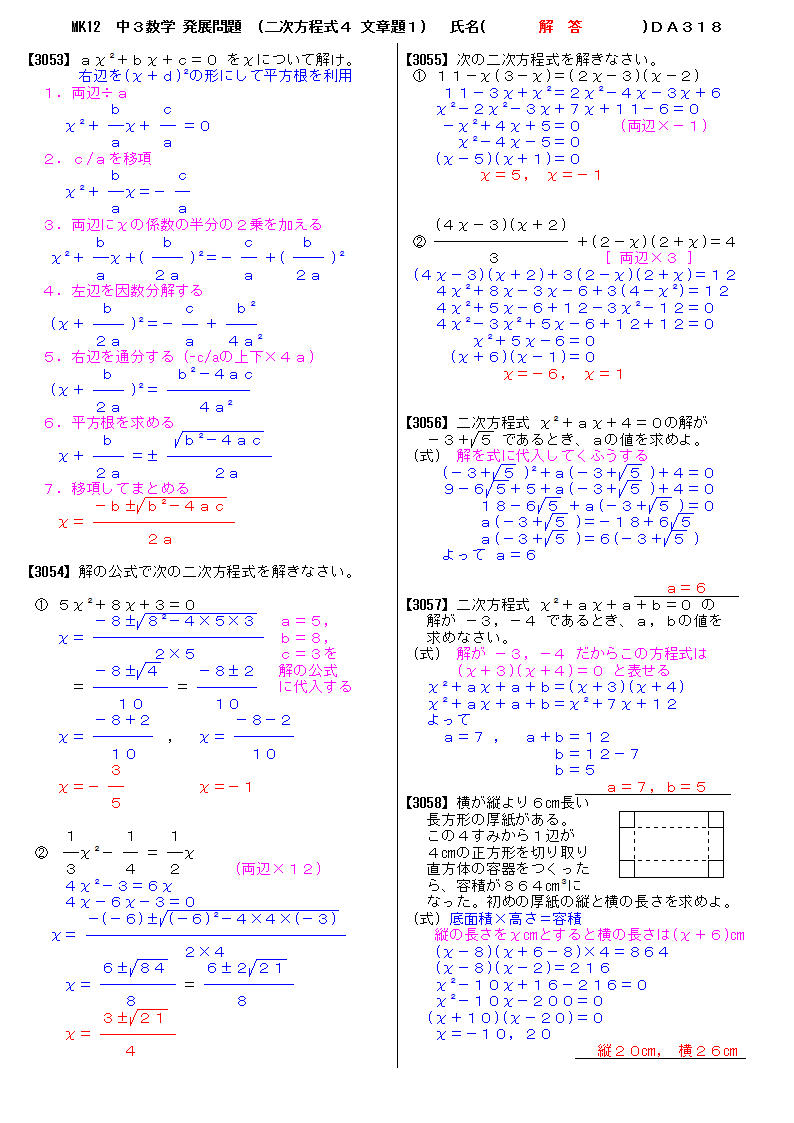方程式 の 応用"> 無料 中３数学 発展 応用問題 解答プリント 318 ２次方程式４ 文章問題１
方程式 の 応用"> 方程式の応用問題 新 心のサプリ 海原純子のharvard Diary
方程式 の 応用"> 二次方程式の解き方 少しだけ応用した平方根の問題 中学や高校の数学の計算問題
方程式 の 応用"> 中学数学 １次方程式 文章題の解き方 代金 個数
方程式 の 応用"> 微分方程式 現代応用数学の基礎 笠原 晧司 本 通販 Amazon
方程式 の 応用"> 6 連立方程式の応用 3 やすこぶたの勉強部屋中２
方程式 の 応用"> Amazon Co Jp 中学 数学 1年 応用 問題集 3 方程式 Dvd 授業 テキスト 問題集 プロ家庭教師が教える 中学生用学習dvd 中学受験 予習 復習 試験対策 Dvd Rom Dvd
方程式 の 応用"> 中学２年生 数学 連立方程式の活用 文章題 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生
方程式 の 応用"> 応用問題 複素数と方程式6 高次方程式 4次相反方程式の解法 No Youtube
高次方程式の応用問題なのですが この式の整理ができません やり方を教えてくだ Yahoo 知恵袋
方程式 の 応用"> 中学数学 １次方程式 文章題の解き方 速さ 時間 道のり
方程式 の 応用"> 中学1年生の数学 一次方程式の文章問題
方程式 の 応用"> 中学２年生 数学 連立方程式の活用 文章題 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生
方程式 の 応用"> 改訂版 クリアー数学b P129 補 直線のベクトル方程式の応用
方程式 の 応用"> 数学ii Bチェック リピート 第5章 2微分法の応用 7 方程式への応用 Pukiwiki
方程式 の 応用"> ７ 連立方程式の応用 4 やすこぶたの勉強部屋中２
方程式 の 応用"> 工学を理解するための応用数学 微分方程式と物理現象 コロナ社
方程式 の 応用"> ベスト 方程式 の 応用 Hd壁紙画像fhd
方程式 の 応用"> 2次方程式の応用問題の解き方 文章問題 数学fun
方程式 の 応用"> 一次不定方程式の解き方とは 応用問題３選もわかりやすく解説します 遊ぶ数学
方程式 の 応用"> 二次方程式の応用 中学三年生 クラス授業 海星学院 泉校 京都府八幡市男山泉3 21
方程式 の 応用"> 数学 B 3次方程式の解と係数の関係の応用 昭和大 東京電機大 青山学院大 星薬科大 大学入試数学の考え方と解法
方程式 の 応用"> ５ 連立方程式の応用 2 やすこぶたの勉強部屋中２
方程式 の 応用"> 高校入試と 連立方程式の応用 係数を求める 中学生 受験対応 英語 数学 学習講座
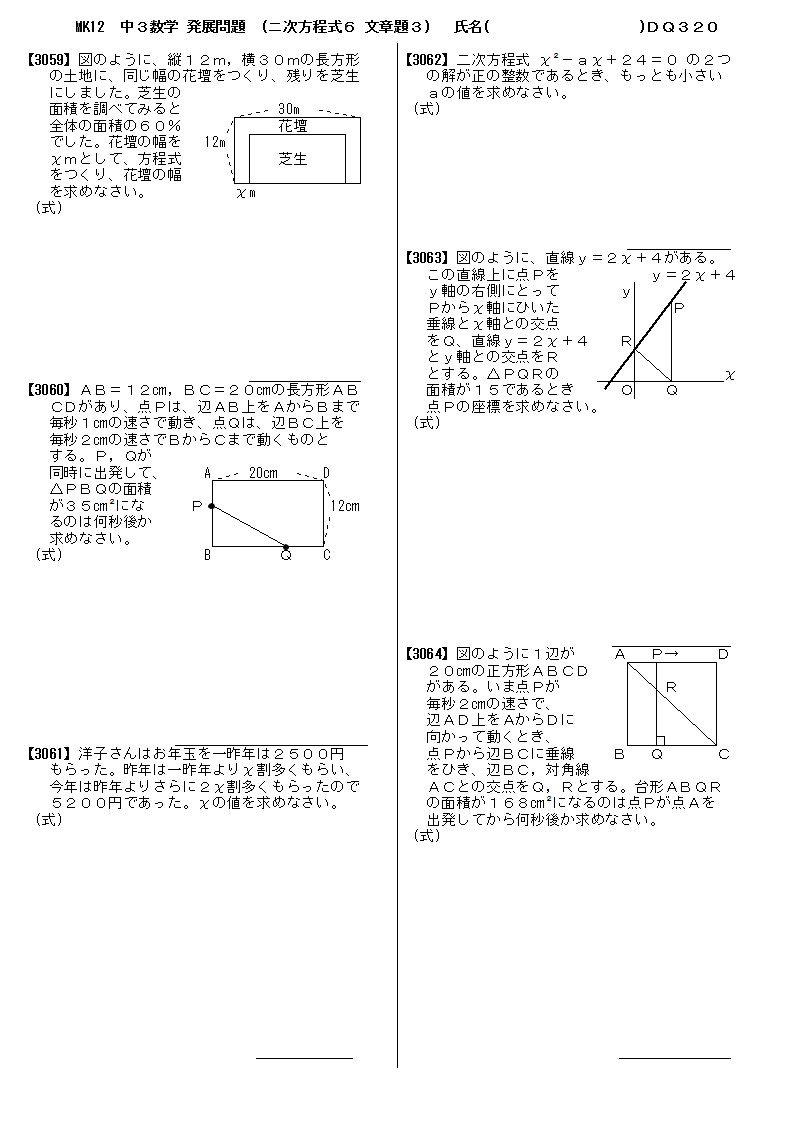
方程式 の 応用"> 無料 中３数学 発展 応用問題 問題プリント 3 ２次方程式６ 文問章題３
方程式 の 応用"> ベクトル方程式の応用最後の Opベクトル Momベクトル N 高校数学に関する質問 勉強質問サイト
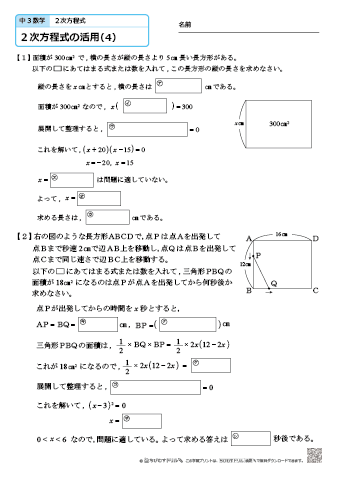
方程式 の 応用"> 中学３年生 数学 ２次方程式の活用 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生
方程式 の 応用"> 中１数学 発展 応用問題プリント 方程式の解き方 124
方程式 の 応用"> 2次方程式 2次不等式の解法と応用パターン 数学の偏差値を上げて合格を目指す
方程式 の 応用"> 高校数学 ２次 ３次方程式の応用問題 ２ 練習編 映像授業のtry It トライイット
方程式 の 応用"> 二次方程式の解がわかっている問題は ｘに代入して計算しよう 中学や高校の数学の計算問題
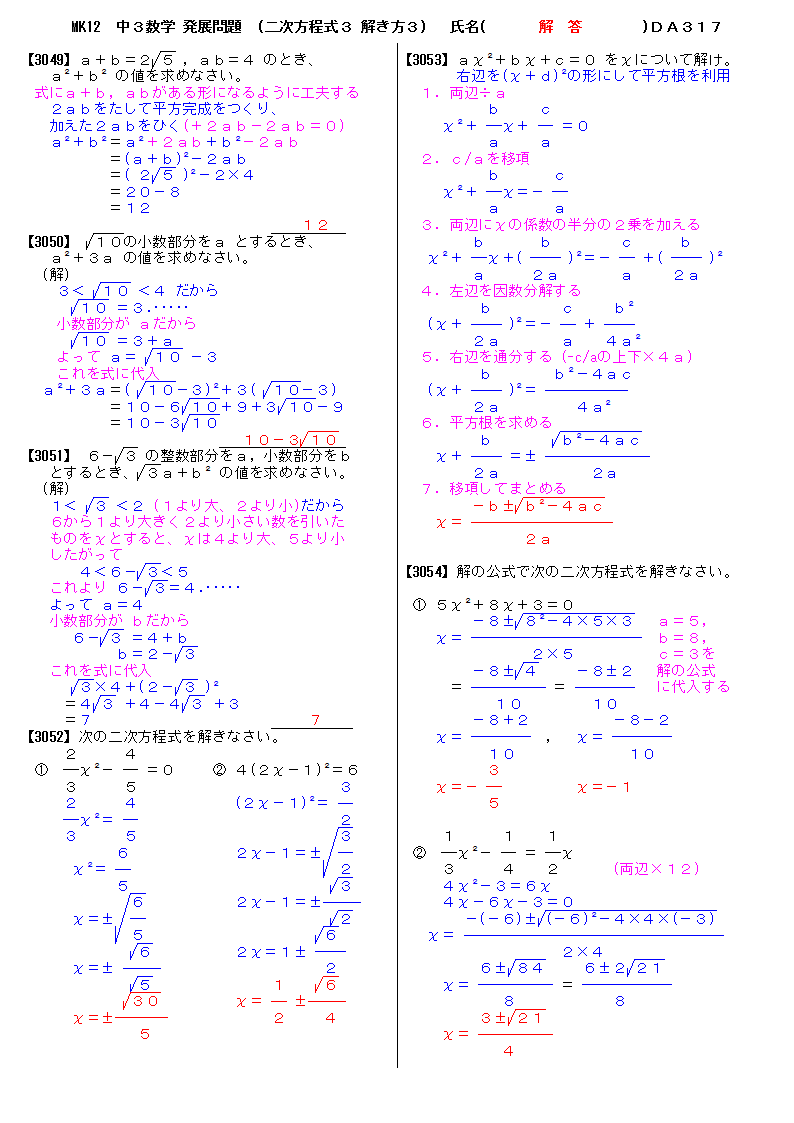方程式 の 応用"> 無料 中３数学 発展 応用問題 解答プリント 317 ２次方程式３ 解き方３
方程式 の 応用"> 連立方程式の応用問題 中学数学 理科 寺子屋塾の復習サイト
方程式 の 応用"> 応用方程式と2進カウンタ
方程式 の 応用"> 改訂版 クリアー数学 P102 40 方程式 不等式への応用
方程式 の 応用"> 連立方程式の応用問題の解き方ー個数 代金編ー Zawanabi ザワナビ
方程式 の 応用"> 100 中2 数学 連立方程式の利用 印刷とダウンロードは無料
方程式 の 応用"> 中学数学 二次方程式の応用 徳島県基礎学力テスト 数樂管理人のブログ
方程式 の 応用"> 方程式の応用について Clear
方程式 の 応用"> 超速まとめ 連立方程式の利用 応用問題 平均 池 鉄橋とトンネル 食塩水の移動 比 仕事 Shun Ei Note
方程式 の 応用"> 京都大学応用数学グループのhp
方程式 の 応用"> 連立一次方程式の応用 Jsciencer
方程式 の 応用"> 高校数学 対数方程式2パターン 受験の月
方程式 の 応用"> 高校数学 ２次 ３次方程式の応用問題 １ 映像授業のtry It トライイット
方程式 の 応用"> 応用微分方程式 学術図書出版社 大学 短大 高専 専門学校向けの教科書出版
方程式 の 応用"> Loewner方程式の応用について Applications Of Loewner Equation
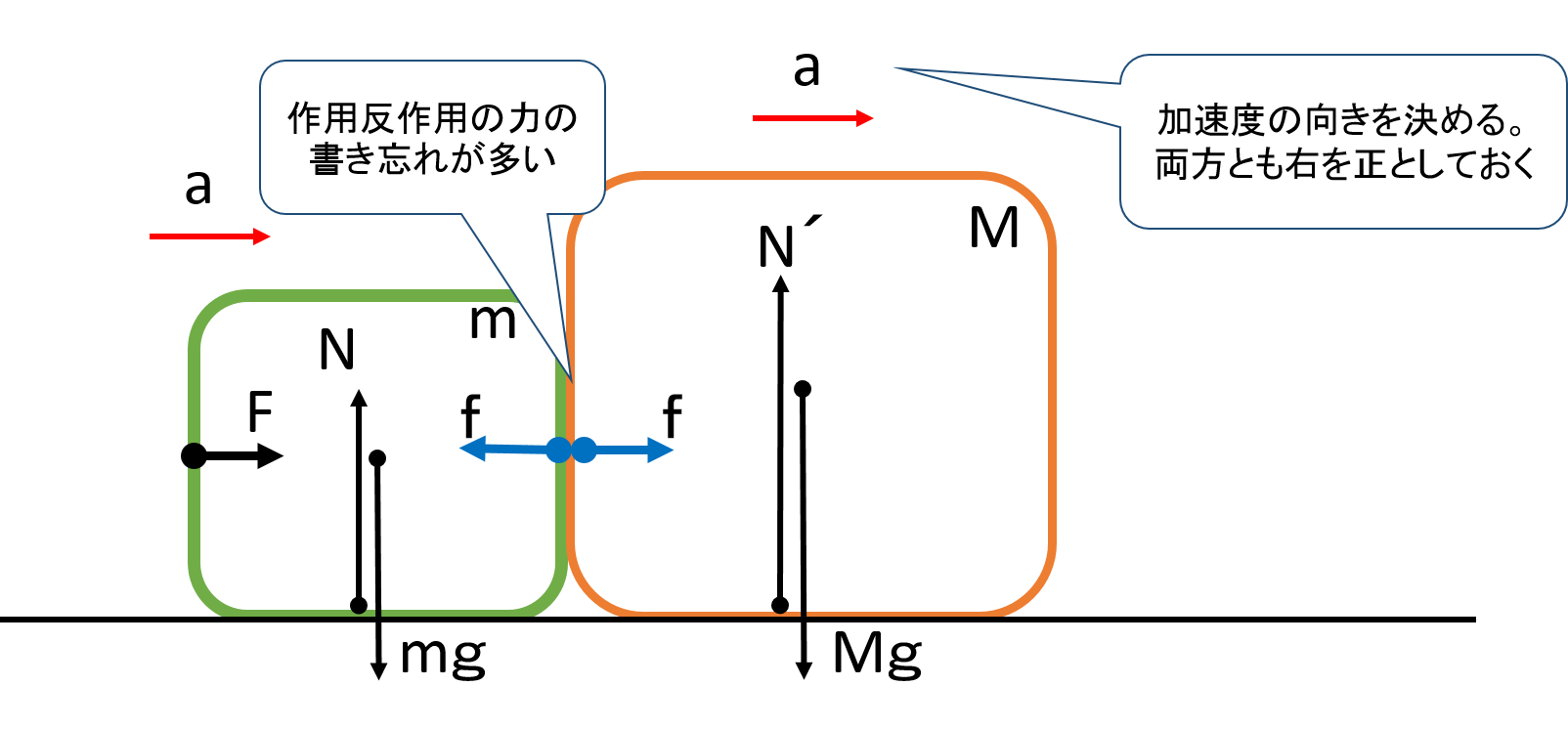
方程式 の 応用"> 物理基礎 運動方程式 応用編 ２物体の解き方は手順を守れば解ける 平川ブログ
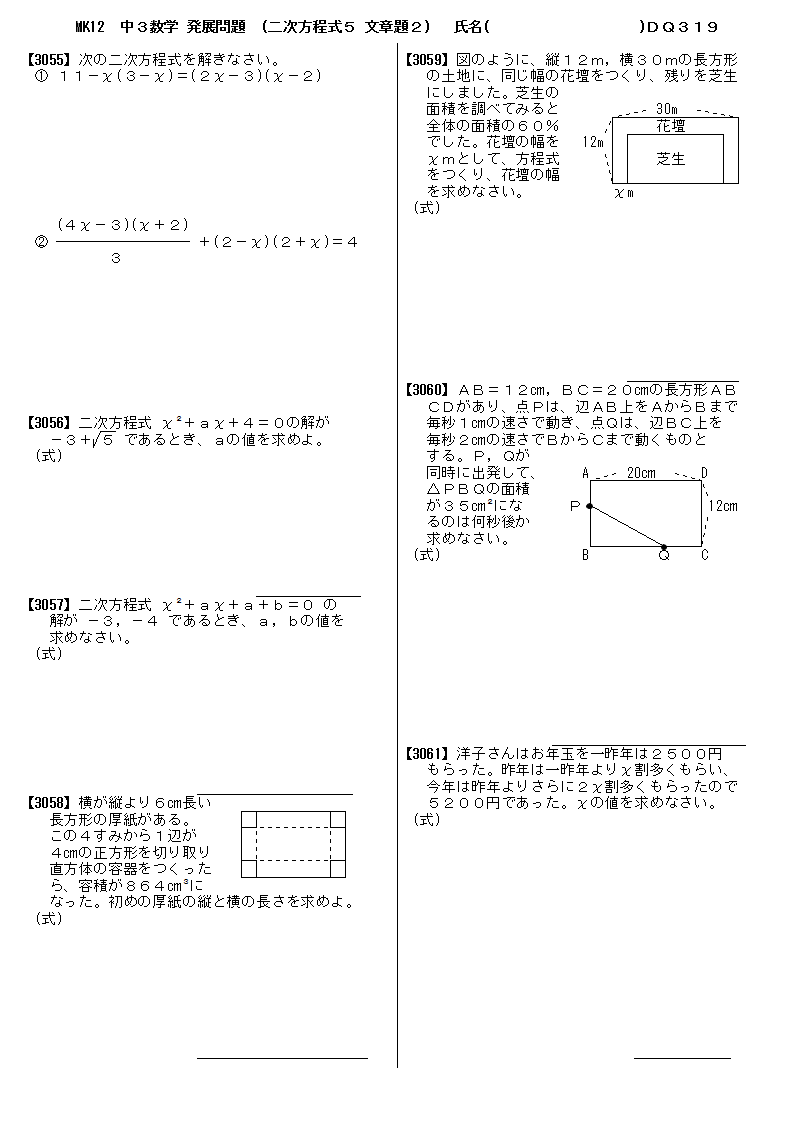
方程式 の 応用"> 無料 中３数学 発展 応用問題 問題プリント 319 ２次方程式５ 文章問題２
方程式 の 応用"> 確率微分方程式とその応用 泰明 兼清 本 通販 Amazon
方程式 の 応用"> 連立方程式の応用問題です わからないので教えて下さい 写真見づらくてすみません Clear
方程式 の 応用"> 数学iiiチェック リピート 第4章 2微分法の応用 5 方程式への応用 Pukiwiki
方程式 の 応用"> 中学３年生 数学 ２次方程式の活用 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生
方程式 の 応用"> 数学 中2 22 連立方程式の利用 みはじの応用編 Youtube
方程式 の 応用"> 中学数学 二次方程式の応用問題 規則性 数樂管理人のブログ
方程式 の 応用"> 合同式 Mod を応用して京大入試問題を解こう 不定方程式の問題も解説 遊ぶ数学
方程式 の 応用"> 連立方程式の応用問題 ダウンロード提供 基本から難問まで 駿英家庭教師学院
方程式 の 応用"> 中学数学 二次方程式の応用問題の解答 設問６ 西美濃 算数 数学教室
方程式 の 応用"> 数学 A 2次方程式の応用問題 Math Master たっくんの数学読書教室
方程式 の 応用"> 中学数学 二次方程式の応用問題の解答 設問１０ 西美濃 算数 数学教室
方程式 の 応用"> 中学２年生 数学 連立方程式の活用 文章題 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生
0 件のコメント:
コメントを投稿